こんにちは、専門学校教員で
理学療法士のダイ吉です!
令和2年2月に行われた、第55回理学療法士国家試験では、今までの前提が覆ることが起こりました。
それは、午前の1発目の実地問題に、統計学の問題が出されたことです。

え、統計学…?

ビックリするよね。
毎年、MMTかROMの絵問題が定番でしたが、いきなり統計学用語の問題とは驚きです。
そこで今日は、同じような問題が出た時のために、この問題を振り返ってみましょう!
検査精度について
最近では、コロナ禍の影響により、検査結果について敏感になってます。
でも実は、検査というのは100%の正確性はなく、色々な誤検出があるんですよね。
まずは、その精度を表す言葉の解説です!
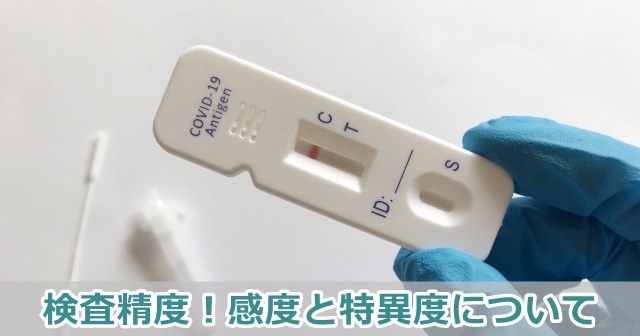
感度とは
感度というのは、ウィルスを持っている人を、正しく陽性と検出する精度です。
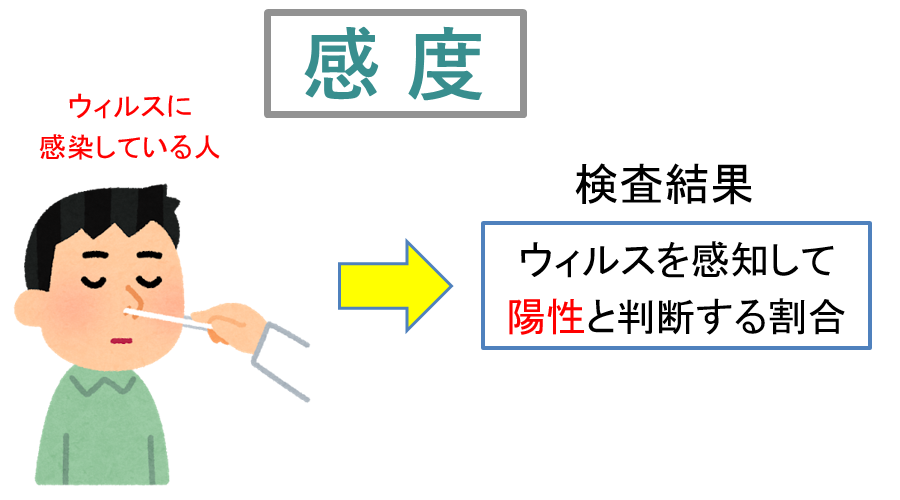
感度100%であれば、ウィルスは絶対に見落とさないという意味になります。
しかし、感度が70%まで下がると、10回に3回はウィルスを見落とすことになります。
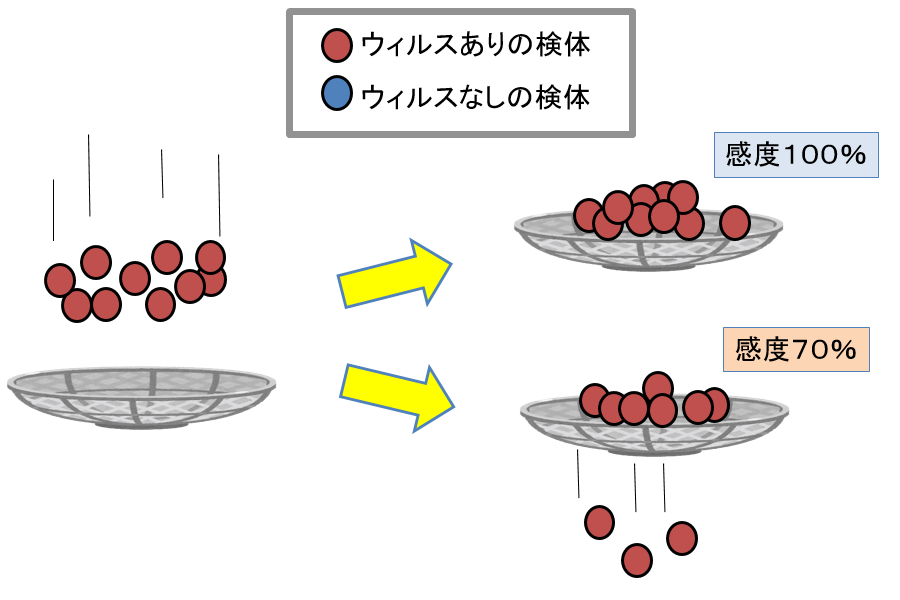
特異度とは
反対に特異度とは、健常者に対して、正しく「陰性」という判断をする精度になります。
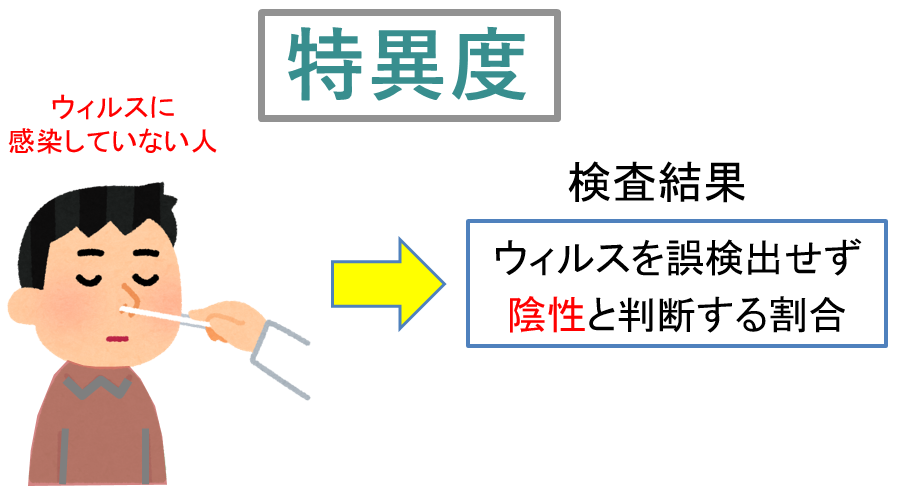
よって、特異度100%であれば、ウィルスを持っていない人には無反応ということです。
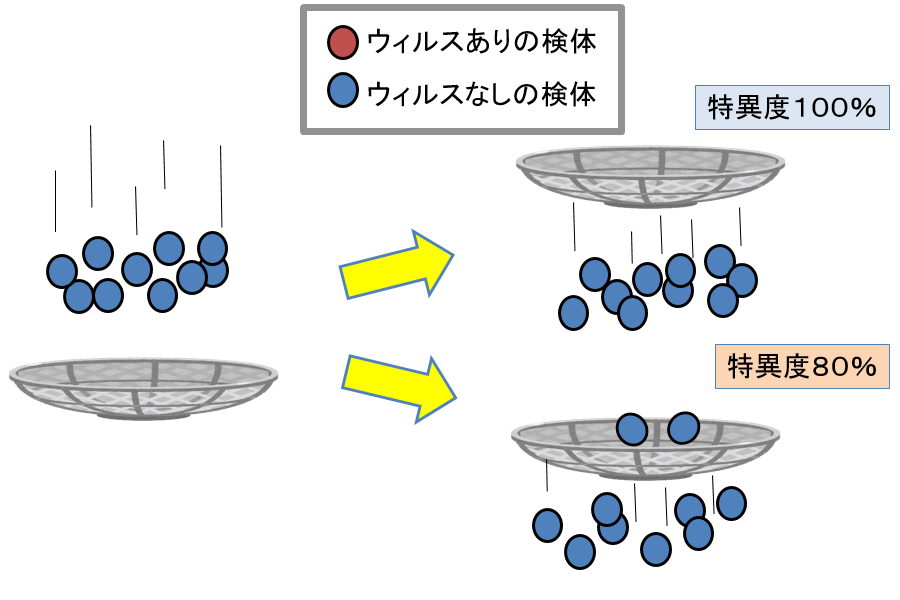
ただし、特異度が80%であれば、10回に2回は健常者に対してウィルスあり!と誤検出することになります。
検査精度の判定方法
感度と特異度が分かったら、実際に検査精度を確認してみましょう。
ウィルスありとなしの検体を10個ずつ、感度80%、特異度60%の精度で検査した時は、陽性となる球の数はどうなりますか?


えっと、80%だから…。

陽性は何個?

答えは、ウィルスありの検体が正しく陽性となる球が8個、ウィルスないのに陽性と誤検出された球が4個です。

あれ、赤と青の球が
混ざってるね?

うん、どっちも100%
じゃないからね。
では、その誤検出について触れていきます。
2種類の陽性と陰性
実は陽性と陰性は2種類ずつあります。
✅ 真陽性
ウィルスを持っていて陽性となる
✅ 偽陽性
ウィルスを持っていないのに陽性となる
✅ 真陰性
ウィルスを持っていないので陰性となる
✅ 偽陰性
ウィルスを持っているのに陰性となる
よって、先ほどの検査精度であれば、以下のように分類することができます。
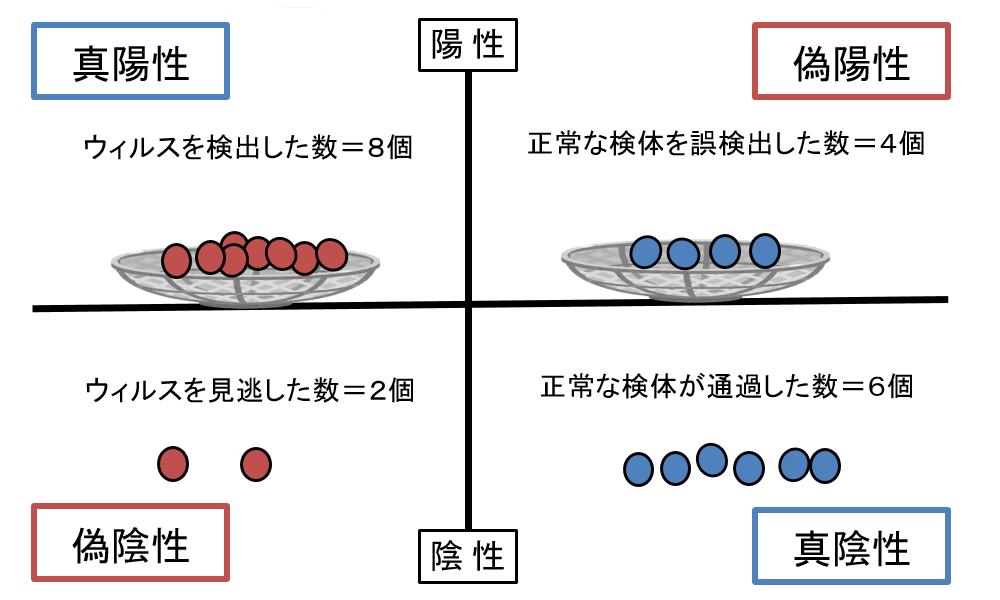

間違った検出結果だと、
色々な不利益が起こるね。

う~ん、偽陰性だった場合、
感染拡大につながるね。

的中率の計算方法
先ほどの解説では、感度は真陽性と偽陰性、特異度は偽陽性と真陰性の割合でしたね。
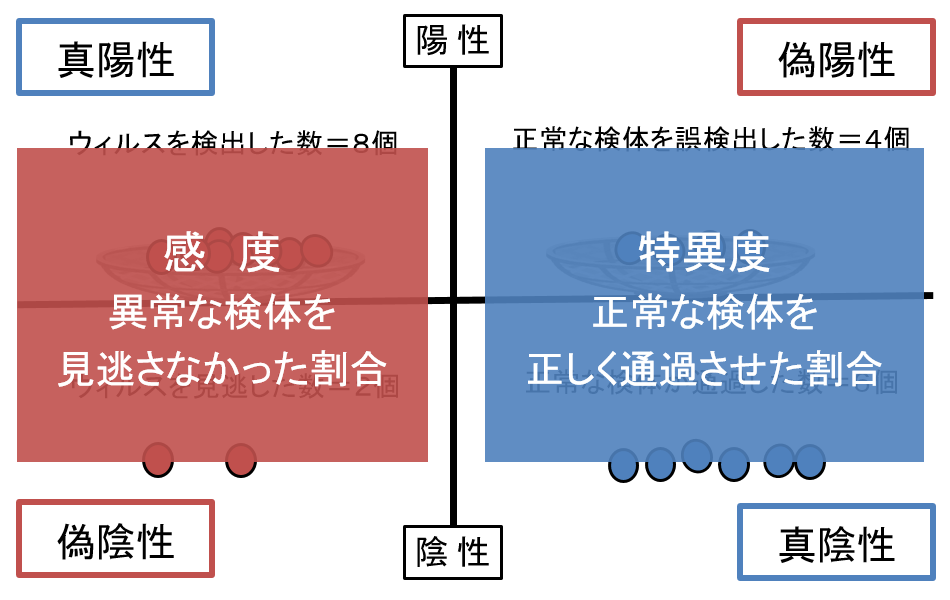
今度は、組み合わせを変えてみましょう。
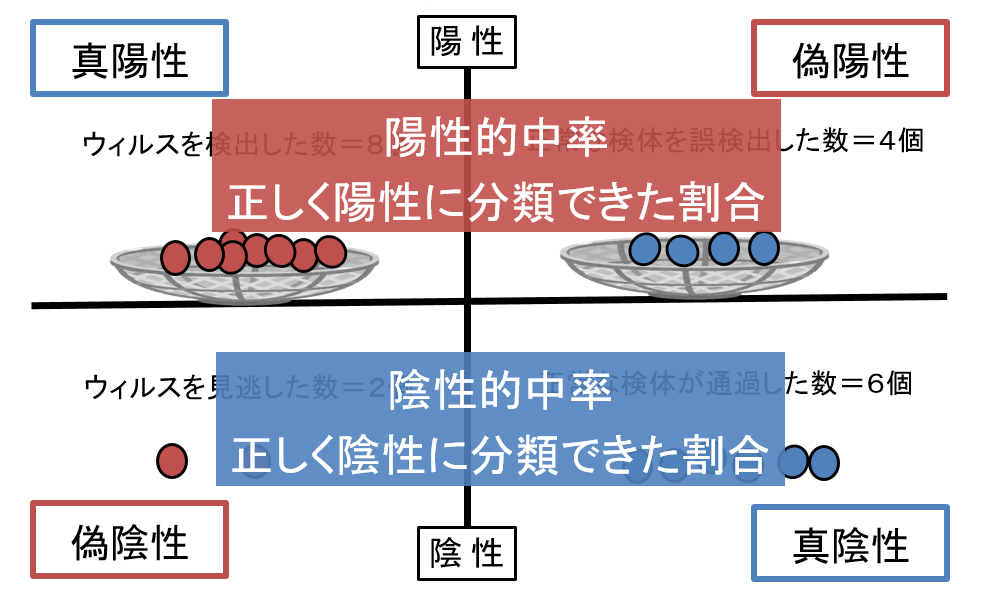
陽性と判断された総数から、本当に陽性だった数の割合を計算してみましょう。
また、陰性と判断された総数から、本当に陰性だった数の割合も計算して下さい。
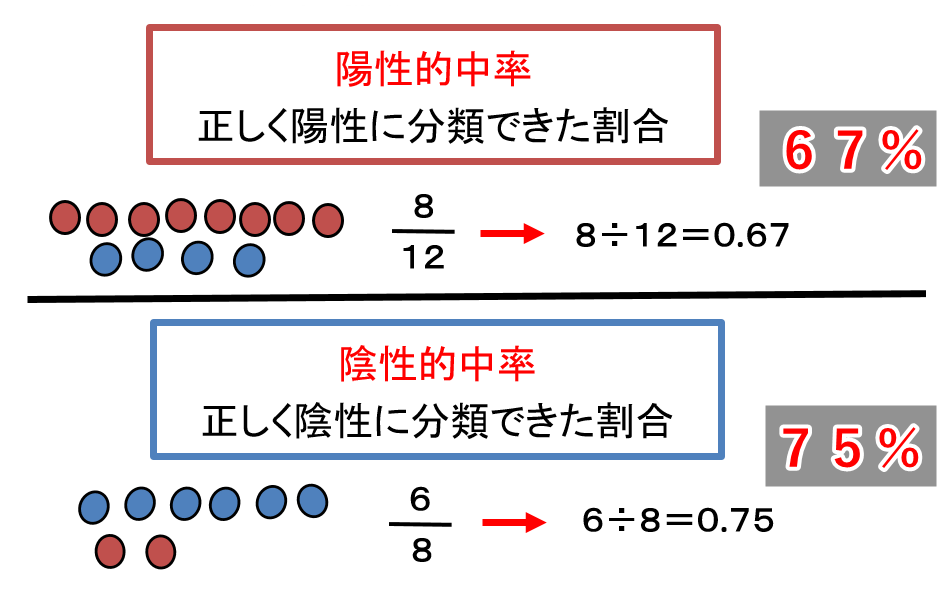
このように、陽性結果の正確性と陰性結果の正確性が、それぞれ分かりましたね。
さて、ここまで分かれば、もう検査精度に関する統計学の勉強は終わりです!

あれ、これだけでいいの?

うん、これで問題は解けるよ!
第55回午前1の解説
では、多くの受験生のメンタルを削った、実際に出題された問題を解いてみましょう。
【問題】
病気Xの有無を調べる検査の感度、特異度、陽性的中率、陰性的中率を表に示す。正しいのはどれか。2つ選べ。
感度 80% 特異度 95% 陽性的中率 85% 陰性的中率 90% 1.病気Xに罹患している人で、検査が正しく陽性と判定された確率は85%である。
2.病気Xに罹患していない人で、検査が正しく陰性と判定された確率は95%である。
3.病気Xを判定する検査が陽性の場合、真に病気Xに罹患している確率は80%である。
4.病気Xを判定する検査が陰性の場合、真に病気Xに罹患している確率は15%である。
5.病気Xを判定する検査が陰性の場合、真に病気Xに罹患していない確率は90%である。

あれれ、これ難しくね?

実はこれ、日本語力を問う
問題なのよね。
さて、まずは情報を整理してみましょう。
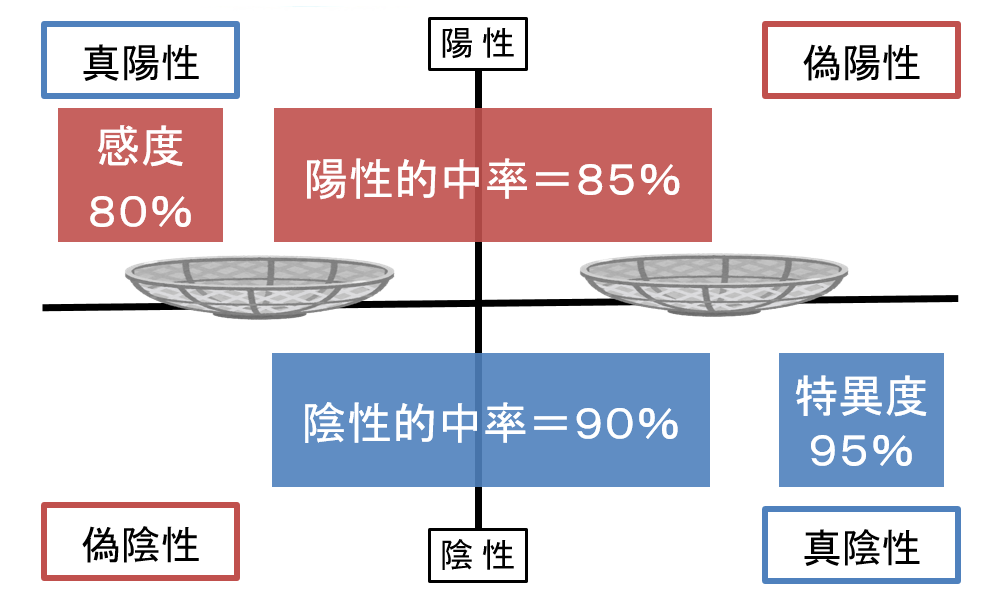
まず選択肢1は、感度は85%か?と聞いています。正しくは80%なので不正解ですね。
選択肢2では、特異度は95%か?と聞いています。特異度は95%と書かれているので正解となります。。

ゆっくり考えると
意外と簡単かも~!
では選択肢3です。
陽性と判定されたうち、本当に陽性だった人、要するに陽性的中率は80%か?と聞いています。当然ですが×ですね。
選択肢4は、陰性と判定されたうち、偽陰性は15%だったの?と聞いています。
偽陰性の割合は、陰性の総数100%から、的中率90%を引いた10%なので不正解。
選択肢5は、陰性的中率は90%か?と聞かれているので正解となります!

ということで、2と5
が正解になるよ!
慣れるまで、あれ?って戸惑うけど、落ち着いて考えれば3点取れる問題でしたね。
ということで、感度と特異度は覚えとこう!
おわりに

さて、あまり出ないけど、取りこぼすのは勿体ない、統計学のお話でした。
検査精度については、何かとニュースで話題になるので、これを気に用語くらいは暗記しておきましょう。

それでは、国家試験の問題に
検査精度が出ますように!

↓【PT国家試験の受験生向けnote】↓